一、填充有两种规则
只要是路径填充,都有两种规则,nonzero和evenodd,无论是SVG中的路径填充,还是Canvas中的路径填充,如果还有其他和路径相关的技术(甚至设计软件),也离不开这两种填充规则。
换句话说,这是超越各种语言,普世通用的技能点。
下面,看看我能不能用足够精简的语言,尽可能让大家都搞懂这两种路径填充规则。
如果我们用3个点,连成一个三角形,则这两种填充规则没什么区别,如下对比(Canvas语法举例,JS实时渲染,如果无效果,请访问原文)。
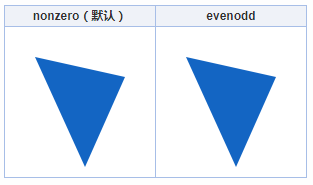
如果是两个三角形,并且发生重叠,差异就出现了,如下:
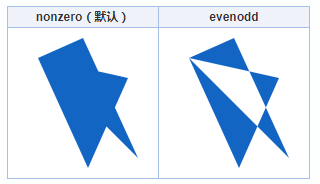
究竟是如何作用的呢?且看~
二、一切都是交叉点们的选择
填充规则的关键,就是确定复杂路径构成的图形,哪些是内部,哪些是外部。内部则填充,外部则透明。
- “
nonzero规则”顾名思意就是“非零规则”,用通俗的话讲,就算计算某些东西是不是0,如果不是0则内部,填充;如果是0则外部,不填充。 - “
evenodd规则”顾名思意就是“奇偶规则”,用通俗的话讲,就算计算某些东西是不是奇数,如果是是奇数则内部,填充;如果是偶数则外部,不填充。
下面关键来了,这里的“计算某些东西”究竟计算的是什么东西呢?
nonzero规则和evenodd规则计算的东西还不一样,nonzero是计算顺时针逆时针数量,evenodd是交叉路径数量。
为了示意更加直观,我们可以把本文示意的三角路径方向和序号标记下,如下表:
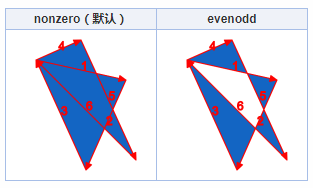
接下来,高能来了……
我们要判断某一个区域是路径内还是路径外,很简单,在这个区域内任意找一个点,然后以这个点为起点,发射一条无限长的射线,然后——
- 对于nonzero规则:起始值为0,射线会和路径相交,如果路径方向和射线方向形成的是顺时针方向则+1,如果是逆时针方向则-1,最后如果数值为0,则是路径的外部;如果不是0,则是路径的内部,因此被称为“非0规则”。
一图胜千言:
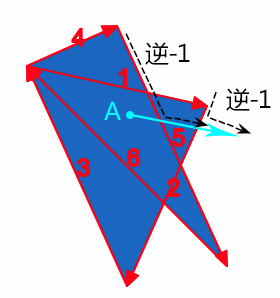
非零规则计数示意
例如上图点A,我们随便发出一条射线,结果经过了路径5和路径2,我们顺着路径前进方向和射线前进方向,可以看到,合并后的运动方向都是逆时针,逆时针方向-1,因此,最后计算值是-2,不是0,因此,是内部,fill时候可以被填充。
再看外部的例子,一图胜千言+1:
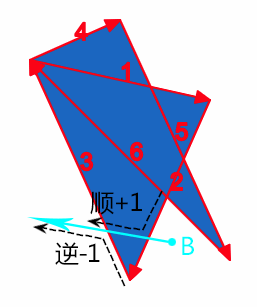
非零规则路径外示意
点B再发出一条射线,经过两条路径片段,为路径2和路径3,我们顺着路径前进方向和射线前进方向,可以看到,合并后的运动方向一个是逆时针,-1,一个是顺时针,+1,因此,最后的计算值是0,是外部,因此,不被填充。
- 对于evenodd规则:起始值为0,射线会和路径相交,每交叉一条路径,我们计数就+1,最后看我们的总计算数值,如果是奇数,则认为是路径内部,如果是偶数,则认为是路径外部。
一图胜千言+2:
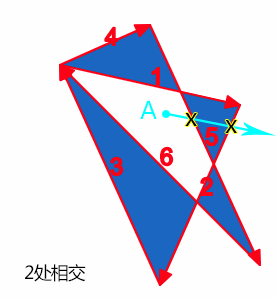
例如上图点A,我们随便发出一条射线,结果经过了路径5和路径2,交叉的路径个数为2,是偶数,因此,属于路径外,不填充。
一图胜千言+3:
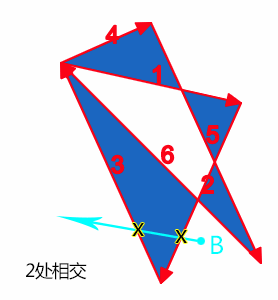
点B再发出一条射线,经过路径片段路径2和路径3,交叉的路径个数为2,是偶数,因此,也属于路径外,不填充。
一图胜千言+4:
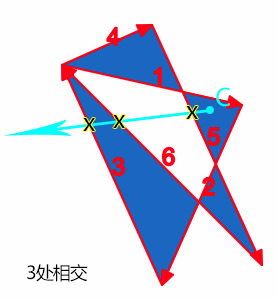
最后这个点C,发出的射线总共和3个路径交叉,是奇数。因此,属于路径内,填充。